miércoles, 5 de diciembre de 2018
martes, 27 de noviembre de 2018
prueba de hipotesis para la media, la varianza y proporciones
En vez de estimar el valor de un parámetro, a veces se debe decidir si una afirmación relativa a un parámetro es verdadera o falsa. Es decir, probar una hipótesis relativa a un parámetro. Se realiza una prueba de hipótesis cuando se desea probar una afirmación realizada acerca de un parámetro o parámetros de una población.
Una hipótesis es un enunciado acerca del valor de un parámetro (media, proporción, etc.).
Prueba de Hipótesis es un procedimiento basado en evidencia muestral (estadístico) y en la teoría de probabilidad (distribución muestral del estadístico) para determinar si una hipótesis es razonable y no debe rechazarse, o si es irrazonable y debe ser rechazada.
La hipótesis de que el parámetro de la población es igual a un valor determinado se conoce como hipótesis nula. Una hipótesis nula es siempre una de status quo o de no diferencia.
En toda prueba de hipótesis se presentan 3 casos de zonas críticas o llamadas también zonas de rechazo de la hipótesis nula, estos casos son los siguientes:
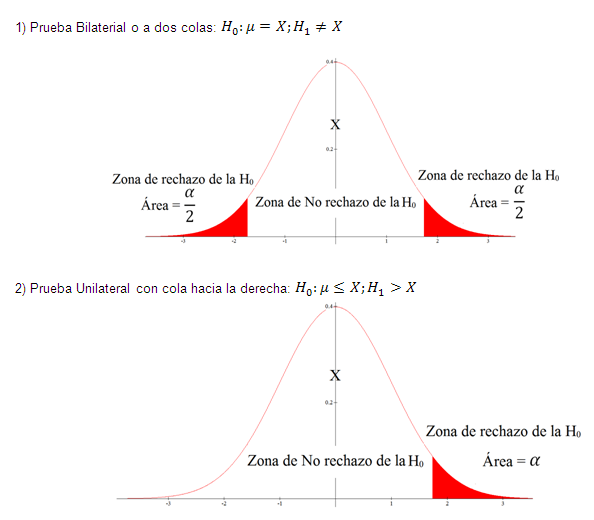
En toda prueba de hipótesis se pueden cometer 2 tipos de errores:
miércoles, 10 de octubre de 2018
estimador
La
inferencia estadística es la colección de técnicas que permiten formular
inferencias inductivas acerca de una característica de una determinada
población sobre la base de la información que contiene la muestra observada, y
que proporcionan una medida del riesgo de éstas.
Pues
bien, expuesta la anterior definición, trabajar con la muestra al completo y de
forma exhaustiva no es fácil ni cómodo. Ello se puede comprobar sin más que
imaginarse un listado de páginas y páginas sobre alturas de los habitantes de
una determinada localidad para tratar de determinar (a partir de ellas) la
altura media de los habitantes de dicha localidad (el parámetro sobre el cual
se quieren llevar a cabo las inferencias).
miércoles, 26 de septiembre de 2018
T-STUDENT
Supóngase que se toma una muestra de una población normal con media 
y varianza 
. Si 
es el promedio de las n observaciones que contiene la muestra aleatoria, entonces la distribución 
es una distribución normal estándar. Supóngase que la varianza de la población 
2 es desconocida. ¿Qué sucede con la distribución de esta estadística si se reemplaza por s? La distribución t proporciona la respuesta a esta pregunta.
La media y la varianza de la distribución t son
= 0 y 
para 
>2, respectivamente.
La siguiente figura presenta la gráfica de varias distribuciones t. La apariencia general de la distribución t es similar a la de la distribución normal estándar: ambas son simétricas y unimodales, y el valor máximo de la ordenada se alcanza en la media = 0. Sin embargo, la distribución t tiene colas más amplias que la normal; esto es, la probabilidad de las colas es mayor que en la distribución normal. A medida que el número de grados de libertad tiende a infinito, la forma límite de la distribución t es la distribución normal estándar.
y varianza . Si es el promedio de las n observaciones que contiene la muestra aleatoria, entonces la distribución es una distribución normal estándar. Supóngase que la varianza de la población 2 es desconocida. ¿Qué sucede con la distribución de esta estadística si se reemplaza por s? La distribución t proporciona la respuesta a esta pregunta.La media y la varianza de la distribución t son
= 0 y para >2, respectivamente.La siguiente figura presenta la gráfica de varias distribuciones t. La apariencia general de la distribución t es similar a la de la distribución normal estándar: ambas son simétricas y unimodales, y el valor máximo de la ordenada se alcanza en la media
= 0. Sin embargo, la distribución t tiene colas más amplias que la normal; esto es, la probabilidad de las colas es mayor que en la distribución normal. A medida que el número de grados de libertad tiende a infinito, la forma límite de la distribución t es la distribución normal estándar.
Suscribirse a:
Comentarios (Atom)